Email format error
Email cannot be empty
Email already exists
6-20 characters(letters plus numbers only)
The password is inconsistent
Email format error
Email cannot be empty
Email does not exist
6-20 characters(letters plus numbers only)
The password is inconsistent

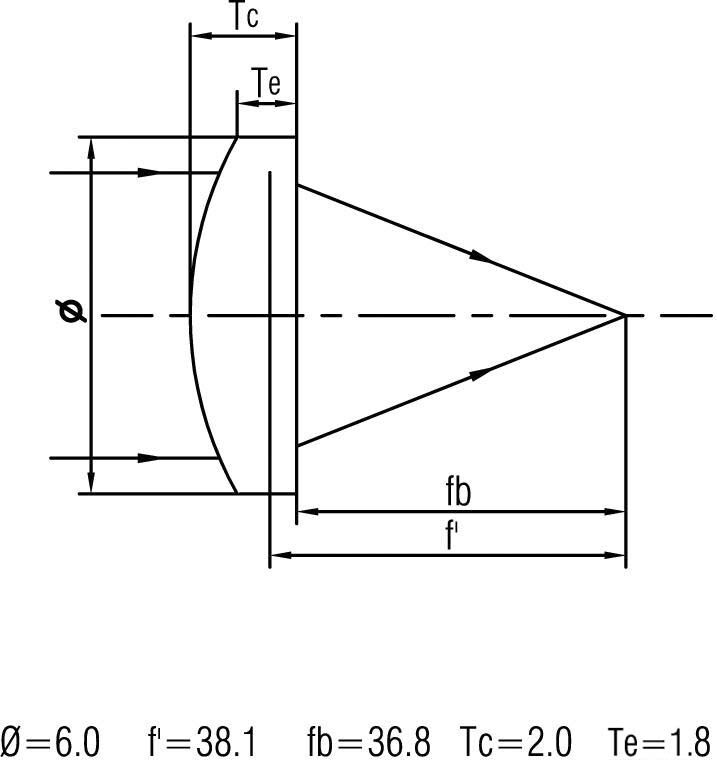
Plano-convex Lens
The imaging principle of a convex lens is as follows: A convex lens is a converging lens, which converges the rays in its front view and diverged at its rear view. When light passes through it, the distance between the front surface and the rear surface will decrease; The focal point of the convex lens is on the principal axis and closer to the first surface than to the second surface.
In the optical industry, the optical lens is the most common optical component, while the convex lens is particularly common and widely used. What exactly is a convex lens?
A convex lens is a lens with a thick center and thin edge. A convex lens has the function of converging light, so it is also called a converging lens, or a positive lens. This kind of lens generally has a biconvex lens, which is a biconvex lens; There is also a flat-convex lens, which has a convex surface on one side and a flat optical lens on the other side; a Concave-convex lens is a lens with one side convex and the other side concave.
Now let's learn what the imaging principle of a convex lens is.
Generally, the imaging law of the convex lens refers to that the object being placed outside the focus and forming an inverted real image on the other side of the convex lens. There are three kinds of real images: reduction, equal size, and amplification.
The smaller the object distance, the larger the image distance, and the larger the real image. The object is placed in the focus and forms an upright magnified virtual image on the same side of the convex lens. The smaller the object distance is, the smaller the image distance is, and the smaller the virtual image is. In optics, the image formed by the convergence of actual light is called a real image, which can be presented by a light screen; On the contrary, it is called a virtual image, which can only be felt by the eyes.
When talking about the difference between real images and virtual images, we often mention such a distinguishing method: "real images are inverted, while virtual images are upright.
”The so-called "upright" and "handstand" are, of course, relative to the original object. Generally, the connecting line between the spherical centers of the two spheres of a convex lens is called the main optical axis of the lens. Therefore, parallel light rays are injected into the convex lens parallel to the main optical axis. After two refractions on both sides of the lens, the light is concentrated at a point on the axis, which is called the focus of the convex lens. The convex lens has a real focus on both sides of the lens. If it is a thin lens, the distance between the two focuses and the center of the lens is roughly the same.
The focal length of a convex lens refers to the distance from the focal point to the center of the lens, usually expressed in F. The smaller the spherical radius of a convex lens, the shorter the focal length. A convex lens can be used for the main axis of magnifying glasses, presbyopia and hyperopia glasses, cameras, movie projectors, microscopes, and telescopes: the straight line passing through the two spherical centers C1 and C2 of a convex lens is called the main optical axis of a convex lens.
Optical center: the central o point of the convex lens is the optical center of the lens. Focus: the light parallel to the main axis converges on a point F on the main optical axis after passing through the convex lens, which is the focus of the convex lens.
Focal length: the distance from the focus f to the optical center O of the convex lens is called focal length, which is expressed by F. Object distance: the distance from the object to the optical center of the convex lens is called the object distance, which is expressed in U.
Image distance: the distance from the image formed by the object through the convex lens to the optical center of the convex lens is called image distance, which is expressed in V. Imaging formula: 1/u (object distance) +1/v (image distance) =1/f (lens focal length)
Therefore, we can calculate the object distance according to the known focal length and image distance.